Introduction
To borrow money from an issuer and pay it back to the holder is the essence of a bond (the purchaser of a bond). At maturity, the issuer must refund the borrowed "par value" (i.e., when the contract ends). This loan provides the holder with coupon payments based on the annuity formula's payout schedule. These financial payments are considered interest by bondholders but a cost of borrowing by the issuer. To calculate a bond's present value (PV), we add up all of the cash flows we expect from the bond between now and when it matures, and we get our original investment back (the par value). This means that we can use a Microsoft Excel spreadsheet to calculate the present value of a bond with a set principle (par value) that will be repaid at some point in the future.
Method for Determining the PV of a Bond of a Different Type
The bond's financial viability depends on the yearly interest rate, the time horizon (how long until the bond expires), and the interest rate. Whether or whether you need the bond's total face value upon maturity is unimportant.
Interest-Free Bonds
Think about a zero-coupon bond that is $1,000 and matures in 20 years. As the bond's value has declined since it was issued, a 5% discount rate is currently offered by the market to buyers. Here are the steps to take to determine the bond's current value:
The term "rate" here refers to the annual percentage yield on the bond's face value. The interest on this bond is compounded by a "Nper" number of times, where N is the number of compounding periods. The bond we issued will mature in 20 years. The "Pmt" notation stands for the coupon's periodic payment of the face value times the number of periods till redemption. Not much to see. Its "Fv" value represents the bond principal fully repaid on its maturity date. The bond is now trading at the market price of $376.89.
Fixed-Interest Bonds
This bond from Company 1 is for $1,000, has a discount rate of 4%, a 20-year maturity, a 2.5% coupon rate, and a discount date of today. The bond's annual coupon is $25. (0.025 multiplied by 1000). The value of "Pmt" in the Function Arguments Box is $25. This bond has a present negative value; hence its purchase would cost the buyer a negative $796.14. In this case, the cost of such a bond would be $796.14.
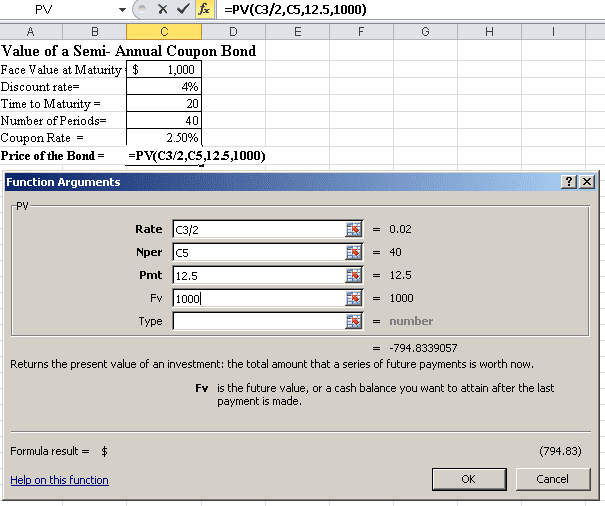
Purchasing Bonds That Pay Interest Twice a Year
A $1,000 face value, 2.5% annual coupon, 20-year maturity, 4% discount, and issued by Company 1. Coupons for this bond are issued annually at a rate equal to $0.0250 x 1000 x $25 x $25 x $12.50. 1.25% (=2.5% 2) is half a percentage point more than twice a year. Since there are 40 6-month intervals throughout a full two decades, "Pmt" is set to $12.50, and "nper" is set to 40 in the Function Arguments Box. At this time, purchasing one of these bonds would result in a loss of $794.83. This bond kind has a price tag of $794.83.
Infinite Compounding Bonds
Continuous compounding occurs when interest is applied to itself at set intervals. We have seen several different options for compounding frequency, including annually, semiannually, and monthly. However, there is no maximum number of compounding periods in continuous compounding. The cash flow is discounted at an exponential rate.
Underhanded Costs
When calculating a bond's "clean price," interest accrued on coupon payments is ignored. When a bond first enters circulation, its price is determined by the primary market. The secondary market price of a bond should reflect the accrued interest since the last coupon payment. The "dirty pricing" of the bond accurately describes this situation. A bond's "Dirty Price" is its Clean Price plus interest accrued. If you add up all of a bond's future interest payments and principal, you get its "Dirty Price." Interest accrued is determined by multiplying the coupon rate by the number of days since the last coupon payment and dividing by the coupon day period.
Conclusion
A convenient Excel formula can be used to price bonds. The PV function can determine the price of a bond with or without annuities and the price of a bond with annual or biannual allowances.




